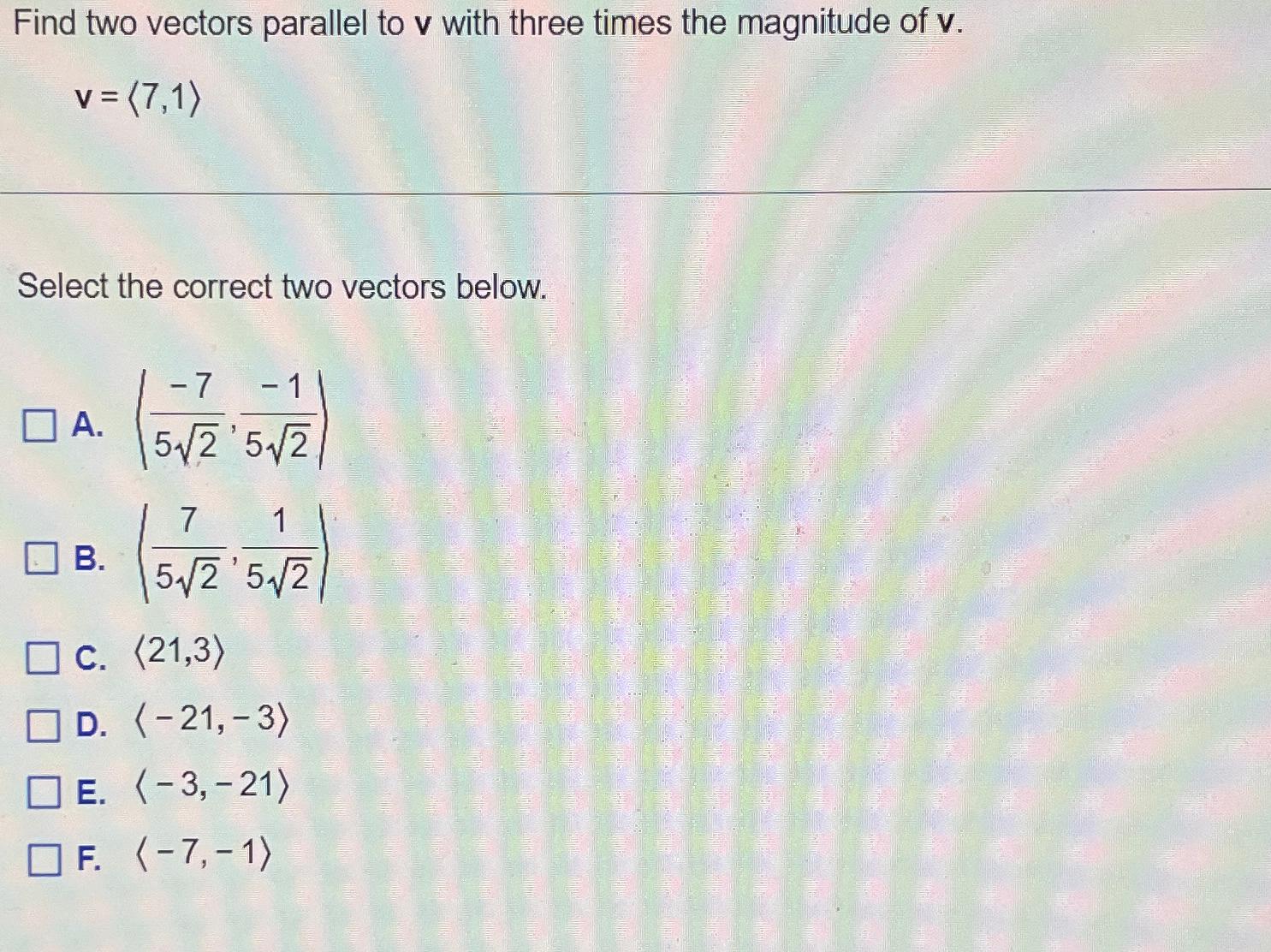
Outstanding Tips About What Happens If Two Vectors Are Parallel

Vectors Aligned
1. Understanding Parallel Vectors
Alright, let's talk vectors! Not the kind that carry diseases, mind you, but the mathematical kind with a magnitude and direction. Now, imagine two of these vectors are hanging out, pointing in the exact same direction (or opposite, but still on the same line). That, my friends, is when we say they're parallel. Think of it like two lanes on a straight highway going the same way, or even trains chugging along on parallel tracks. They might be different lengths (one train could be longer than the other), but they're sharing the same directional vibe.
The key takeaway here is the direction. Parallel vectors have either the same direction or completely opposite directions. This "sameness" is what makes them special and unlocks some cool mathematical properties. For instance, you can always scale one parallel vector to exactly match the other. Want to impress your friends at the next party? Just casually drop that fact.
It's not just about visualization, either. We can rigorously define this with math. If vector a and vector b are parallel, then there exists a scalar (a regular number, like 2 or -5) called 'k' such that a = k b. In simple words, one vector is just a scaled-up or scaled-down version of the other. This 'k' can be positive (same direction) or negative (opposite direction). And if k is zero? Well, then one of your vectors is just the zero vector, a special case that's also considered parallel to everything!
So, next time you see two arrows pointing in the same general direction, give them a second look. Are they perfectly aligned? If so, you've spotted parallel vectors in the wild. Consider yourself a vector whisperer!
What Happens When Vectors Run Parallel?
2. Mathematical Consequences of Parallelism
Okay, so we've established what parallel vectors are , but what's the big deal? What happens when these vectors decide to align themselves? Well, quite a few useful things, actually! Let's start with a bit of linear algebra magic.
One significant consequence involves the determinant of a matrix formed by these vectors. If you create a matrix using parallel vectors as columns (or rows), the determinant of that matrix will always be zero. This is a handy trick for determining linear dependence. If the determinant's zero, the columns (or rows) are linearly dependent, meaning one can be expressed as a linear combination of the others. In the case of two vectors, this directly indicates parallelism.
Another cool thing is the cross product. If you take the cross product of two parallel vectors, you'll always get the zero vector. The magnitude of the cross product is geometrically interpreted as the area of the parallelogram formed by the two vectors. Since parallel vectors can't form a "real" parallelogram (it's just a flat line!), the area is zero, hence the zero vector result. Remember, cross product applies only to 3D space!
From a geometric perspective, parallel vectors simplify many calculations. For example, finding the projection of one vector onto another becomes extremely straightforward. Since they align (or anti-align), the projection's magnitude is simply the scaled component of one vector onto the other. Think of shining a light straight down on one vector — its "shadow" on the other is the projection. Easy peasy!
Applications in the Real World
3. Parallel Vectors in Action
Alright, enough with the abstract math talk! Where do we actually see parallel vectors in the real world? The answer is: everywhere! They pop up in physics, computer graphics, engineering, and even art (though maybe not explicitly labeled "parallel vectors").
In physics, consider forces acting on an object. If two forces are acting in the same direction, they are parallel. Calculating the net force is then a simple addition of their magnitudes (assuming they point in the same direction; subtract if opposite). This is fundamental in understanding how objects move and interact.
In computer graphics, parallel vectors are essential for creating realistic lighting and shading effects. When calculating how light reflects off a surface, the normal vector (a vector perpendicular to the surface) and the light source vector play a crucial role. If the light source vector is parallel (or close to parallel) to the normal vector, the surface will be brightly lit. This helps create a sense of depth and realism in virtual environments.
In engineering, particularly in structural analysis, parallel vectors are crucial for understanding stress and strain. When analyzing the forces acting on a beam or bridge, engineers need to consider the directions of these forces. Parallel forces are much easier to analyze than forces acting at arbitrary angles, simplifying the design process.
Even GPS systems rely on principles related to vectors. Although not directly manipulating "parallel" vectors in the common sense during triangulation, satellite signals and their relative positioning embody vector-like quantities for range and direction calculations.
Dot Product and Angle Between Vectors
4. Delving Deeper into Vector Relationships
Now that we've discussed parallelism, let's connect it to another important concept: the dot product. The dot product is a mathematical operation that takes two vectors and returns a scalar value. This value is closely related to the angle between the vectors, including cases when vectors are parallel.
The dot product of two vectors a and b is defined as |a||b|cos(), where |a| and |b| are the magnitudes of the vectors and is the angle between them. When the vectors are parallel, the angle is either 0 degrees (same direction) or 180 degrees (opposite direction).
If = 0 degrees, then cos() = 1, and the dot product becomes |a||b|, which is simply the product of their magnitudes. If = 180 degrees, then cos() = -1, and the dot product becomes -|a||b|, which is the negative of the product of their magnitudes. This provides a quick way to check if two vectors are parallel: calculate their dot product and compare it to the product (or negative product) of their magnitudes.
Therefore, if you know the magnitudes of the vectors and their dot product, you can determine the angle between them using the formula: = arccos((a b) / (|a||b|)). For parallel vectors, this will always yield either 0 or 180 degrees. Isn't math neat? It's like a secret code to unlock the relationships between geometric objects.
Parallel vs. Collinear Vectors: What's the Difference?
5. Clarifying the Terminology
Here's a detail that sometimes trips people up: the difference between "parallel" and "collinear" vectors. While the terms are often used interchangeably in informal settings, there's a subtle but important distinction to be aware of.
Essentially, collinear means lying on the same line. This encompasses vectors that are parallel, but it also includes points. A collection of points lying on the same line can be described as collinear. Therefore all parallel vectors are collinear, but not all collinear objects are vectors. A single point on a line, or a series of points along a single line are said to be collinear, yet, don't have vector properties. Vectors need magnitude and direction.
Technically, two vectors can be parallel without being collinear if they lie on parallel lines that are distinct. However, in most discussions, particularly within the context of vector algebra and linear algebra, the term "parallel" is used more broadly to include cases where the vectors lie on the same line. It's the direction* that matters most.
So, while technically a distinction exists, don't sweat it too much. Unless you're writing a rigorous mathematical proof, using "parallel" and "collinear" interchangeably when discussing vectors is generally acceptable. Just be mindful of the context and audience.
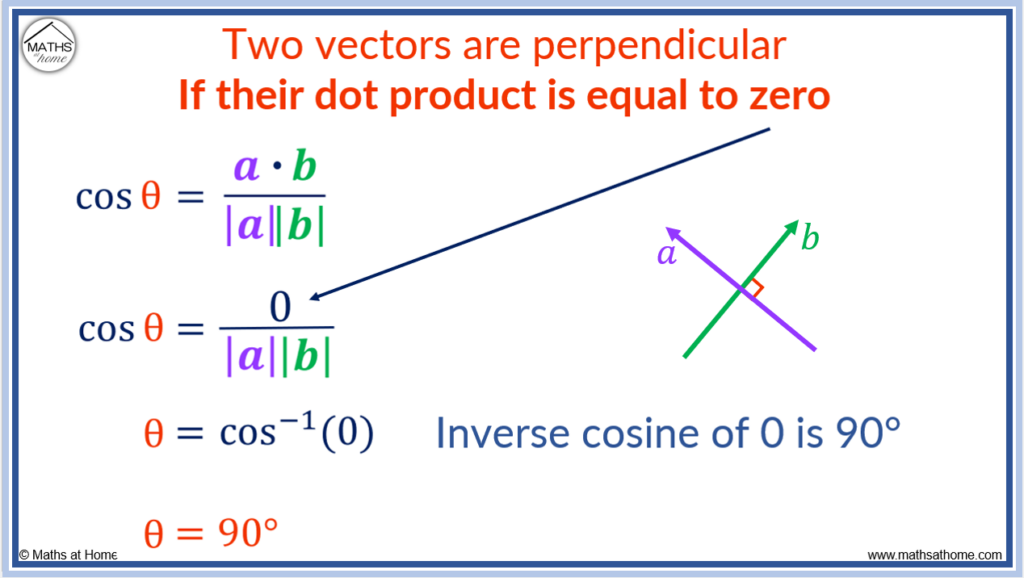
How To Find The Angle Between Two Vectors